どうしても書かきたくなったので、
　　　　　算数さんすうを始はじめるぜ☆　第２話☆

夢美ゆめみ　「りんごが１個このときは、“１”はりんごの個数こすうです」

ちゆり「りんごが１個こだぜ〜☆」






夢美ゆめみ　「りんごが２個こでも、“１”で〜す」

ちゆり「……☆」







夢美ゆめみ　「りんごが３個こでも、“１”で〜す」

ちゆり「……☆」







夢美ゆめみ　「りんごが４個こでも、“１”で〜す」

ちゆり「☆ｗｗｗ」







夢美ゆめみ　「では、りんごが１６個このときは、数字すうじはいくつでしょう？」





ちゆり「んーっ、分わからないぜ、答こたえがいっぱいあるから☆ｗｗｗ」
　　　　　　　　　　　　　　　　　　 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
　　　　この答案用紙とうあんようしは　白紙はくしにしておくか☆ｗｗ」




夢美ゆめみ　「だからあんたは　算数さんすうのテストが０点てんで　持もって帰かえってくるのよ。
　　　　じゃあ、答こたえを１０個書こかきなさいよ」

ちゆり「１つ目めの答こたえは　１　だぜ☆
　　　　理由りゆうはいくつか考かんがえられる☆」





ちゆり「増ふえたりんごの数かずが１という説せつだぜ☆」

ちゆり「設問せつもんで例示れいじされたデータは　順番じゅんばんに並ならんでいて
　　　　前まえの例示れいじの続つづきから後うしろの問題もんだいが始はじまるとするなら、
　　　　１２も答こたえだぜ☆」

ちゆり「数字すうじが１しかない世界せかいでは、数字すうじのどの桁けたを選えらんでも１だな☆
　　　　画面がめんの表示ひょうじが壊こわれていて１桁けたしか出でなくなっているとすれば、答こたえは１だぜ」

ちゆり「りんごというグループが１つ、とも数かぞえられるな☆」

ちゆり「１列れつに並ならんでいたのを正面しょうめんから見みたので、
　　　　レーダーには１つのりんごしか映うつらなかったんだぜ☆」

ちゆり「目めに見みえているりんごは、１つのりんごの鏡かがみに映うつった姿すがただったんだぜ☆
　　　　りんごは１つしかないな☆」

ちゆり「りんごを数かぞえているのではなくて、余白よはくを数かぞえているのだとすれば、
　　　　余白よはくは１個こだな☆」

ちゆり「答こたえは２かもしれないぜ☆

　　　　１ダースの箱はこには１２個このりんごが入はいるな☆
　　　　１６個このりんごなら、２ダースの箱はこが必要ひつようだぜ☆」

ちゆり「あっ☆　消費期限しょうひきげんが残のこり１日にちという説せつも捨すてがたいぜ☆

　　　　１日後にちごには、これらのりんごは一斉いっせいに腐くさりだすんだぜ☆」

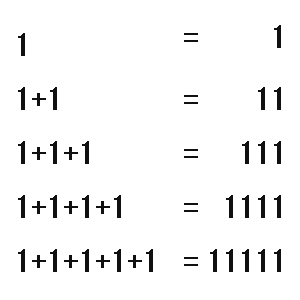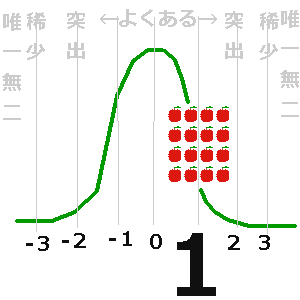
ちゆり「このりんごは　標準偏差ひょうじゅんへんさが１のあたりにいるのかもしれないぜ☆
　　　　つまり　そこらへんに　どこにでもよくある　個性こせいの違ちがいがあんまりない　りんごだな☆」



夢美ゆめみ　「で、どれが　あんたの答こたえなのよ」


ちゆり「えっ……☆　全部ぜんぶが答こたえだぜ☆」


夢美ゆめみ　「１０個こも答こたえが書かいてあったら　先生せんせいの採点さいてんが面倒臭めんどうくさいでしょう！
　　　　私わたしが丸まるを付つけたくなる答こたえを１つ選えらんで答こたえなさい！」


ちゆり「ちょっと待まつんだぜ☆　過去問かこもんを買かってくるぜ☆」





ちゆり「付つけ焼刃やきばっ☆！
　　　　
　　　　………
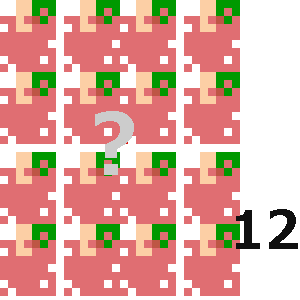
　　　　　　　　少すくなくとも、りんごの右下みぎしたの数字すうじは　りんごの個数こすうではないのだろう☆
　　　　　　　　
　　　　　　　　そして、夢美先生ゆめみせんせいの問題もんだいからは、
　　　　　　　　りんごの数かずが変かわっても　りんごの右下みぎしたの数字すうじが動うごかないことから、
　　　　　　　　りんごの右下みぎしたの数字すうじと、りんごの個数こすうとの間あいだに
　　　　　　　　関連性かんれんせいがあると考かんがえるほうが不自然ふしぜんである☆
　　　　　　　　
　　　　　　　　
　　　　　　　　りんごの右下みぎしたの数字すうじと、りんごの個数こすうとの間あいだに関連性かんれんせいがあるとしても、
　　　　　　　　１　以外いがいになる場合ばあいが分わからない☆
　　　　　　　　
　　　　　　　　そこで、　答こたえ　１　。　としたくなるのが心情しんじょうである☆
　　　　　　　　
　　　　　　　　しかし　夢美先生ゆめみせんせいから戻もどってきた答案とうあんでは　×　であった☆
　　　　　　　　そこで我々われわれは　自分じぶんの席番号せきばんごうを書かくことを口裏合くちうらあわせし、
　　　　　　　　１〜６０の数字すうじを埋うめたが、皆みな　０点レーてん　で補習行ほしゅういきであった☆
　　　　………
　　　　　　　　（ぺらり）
　　　　………
　　　　　　　　
　　　　　　　　
　　　　　　　　１６個このりんごは　４個こ＋４個こ＋４個こ＋４個こ　に分わけることができる☆
　　　　　　　　
　　　　　　　　りんごは　『４個こでも“１”で〜す』　と夢美先生ゆめみせんせいが言いっていることから、
　　　　　　　　この場合ばあい、りんごが１６個このときの不思議ふしぎな数字すうじは　４　である可能性かのうせいがないこともない☆　…　（ａ）
　　　　　　　　
　　　　　　　　
　　　　　　　　また、１６個このりんごは
　　　　　　　　　１個こ＋１個こ＋１個こ＋１個こ＋１個こ＋１個こ＋１個こ＋１個こ＋１個こ＋１個こ＋１個こ＋１個こ＋１個こ＋１個こ＋１個こ＋１個こ
　　　　　　　　に分わけることができる☆
　　　　　　　　
　　　　　　　　『りんごが１個このときは、“１”はりんごの個数こすうです』　と夢美先生ゆめみせんせいが言いっていることから、
　　　　　　　　この場合ばあい、りんごが１６個このときの不思議ふしぎな数字すうじは　１６　である可能性かのうせいがないこともない☆　…　（ｂ）
　　　　　　　　
　　　　　　　　
　　　　　　　　
　　　　　　　　
　　　　　　　　だが　この場合ばあい、（ａ）の主張しゅちょうと（ｂ）の主張しゅちょう、どちらを取とるのかはっきりしない☆
　　　　　　　　
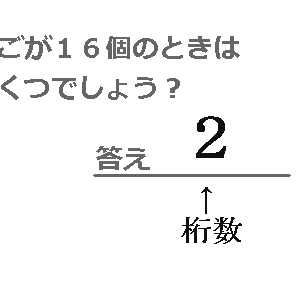
　　　　　　　　そこで、夢美先生ゆめみせんせいは、『りんごが１６個このときは、数字すうじはいくつでしょう？』と、
　　　　　　　　主語しゅごがはっきりしない数字すうじを聞きいているので、
　　　　　　　　
　　　　　　　　不思議ふしぎな数字すうじを　ずばりと言いい当あてるのではなく、
　　　　　　　　可能性かのうせいがないともいえない不思議ふしぎな数字すうじが　いくつ出でてくるのかを聞きいているとも取とれなくもないと、
　　　　　　　　言いい張はることにした☆
　　　　　　　　
　　　　　　　　そこで私わたしは　４〜１６の間あいだで、可能性かのうせいのある全すべての不思議ふしぎな数字すうじを　答案用紙とうあんようしに列挙れっきょした☆
　　　　　　　　
　　　　　　　　４　　＝　４＋４＋４＋４
　　　　　　　　５　　＝　４＋４＋４＋３＋１
　　　　　　　　６　　＝　４＋４＋４＋２＋１＋１
　　　　　　　　７　　＝　４＋４＋４＋１＋１＋１＋１
　　　　　　　　８　　＝　４＋４＋３＋１＋１＋１＋１＋１
　　　　　　　　９　　＝　４＋４＋２＋１＋１＋１＋１＋１＋１
　　　　　　　　１０　＝　４＋４＋１＋１＋１＋１＋１＋１＋１＋１
　　　　　　　　１１　＝　４＋３＋１＋１＋１＋１＋１＋１＋１＋１＋１
　　　　　　　　１２　＝　４＋２＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１
　　　　　　　　１３　＝　４＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１
　　　　　　　　１４　＝　３＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１
　　　　　　　　１５　＝　２＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１
　　　　　　　　１６　＝　１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１
　　　　　　　　
　　　　　　　　４、５、６、７、８、９、１０、１１、１２、１３、１４、１５、１６　の、
　　　　　　　　１３個この不思議ふしぎな数字すうじがある☆
　　　　　　　　
　　　　　　　　
　　　　　　　　よって、答こたえは　１３。
　　　　　　　　すると前例ぜんれいの　１〜６０　の数字埋すうじうめ作戦さくせんに反はんして、
　　　　　　　　これで　わたしは　夢美先生ゆめみせんせいから「惜おしい　−１点マイナスいってん」とのコメント付つきで　９点てんをもらった☆
　　　　　　　　
　　　　………
　　　　
　　　　
　　　　
　　　　先人せんじんおつ☆ｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗ
　　　　思おもってたのと全然違ぜんぜんちがう☆ｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗ」






ちゆり「不自然ふしぜんじゃないか☆ｗｗ
　　　　
　　　　いや、不自然ふしぜんに感かんじるのは　不思議ふしぎの世界せかいの外そとの住民じゅうみんだからで、
　　　　不思議ふしぎの世界せかいの住人じゅうにんには自然しぜんなのかもしらん☆
　　　　
　　　　では、不思議ふしぎな数字すうじが　２〜１２　になるケースも考かんがえてみよう……☆」



ちゆり「いや、そういうことはできないぜ☆
　　　　この数字すうじは、不思議ふしぎな数字すうじが何個なんこでてくるかという“個数こすう”なので、１増ふえたり、１減へったりするのは
　　　　　　　　
　　　　　　　　４　　＝　４＋４＋４＋４
　　　　　　　　５　　＝　４＋４＋４＋３＋１
　　　　　　　　６　　＝　４＋４＋４＋２＋１＋１
　　　　　　　　７　　＝　４＋４＋４＋１＋１＋１＋１
　　　　　　　　８　　＝　４＋４＋３＋１＋１＋１＋１＋１
　　　　　　　　９　　＝　４＋４＋２＋１＋１＋１＋１＋１＋１
　　　　　　　　１０　＝　４＋４＋１＋１＋１＋１＋１＋１＋１＋１
　　　　　　　　１１　＝　４＋３＋１＋１＋１＋１＋１＋１＋１＋１＋１
　　　　　　　　１２　＝　４＋２＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１
　　　　　　　　１３　＝　４＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１
　　　　　　　　１４　＝　３＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１
　　　　　　　　１５　＝　２＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１
　　　　　　　　１６　＝　１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１＋１
　　　　　　　　
　　　　このパターンが４〜１７になったり、４〜１５になることなんだぜ☆
　　　　この計算けいさんは　簡単かんたんじゃないぜ☆／（＾ｏ＾）＼ｗｗｗｗ　はっ☆！！！！！！！！」




ちゆり「５進数しんすうの桁数けたすうじゃないか☆　１０進数しんすうの桁数けたすうでもいけるな☆」









夢美ゆめみ　「エレガントね」



ちゆり「汚きたない丸まるなんだぜ……☆」

ちゆり「設問せつもんが悪わるいんじゃないか☆　幅広はばひろく捉とらえることが　できすぎじゃないか☆ｗ
　　　　いろんな答こたえが当あたっているんじゃないか☆？ｗｗ」


夢美ゆめみ「答こたえが合あっているから丸まるを付つけるかどうかなんて、わたしの気分きぶんで決きめるわよ。
　　　　ぱっと見みて、ぴかっ　とくる解とき方かたがいい答こたえなのよ」


ちゆり「問題もんだいがありそうなんだぜ☆ｗｗｗｗｗｗｗｗｗｗｗ」


夢美ゆめみ　「素敵すてきかどうかがポイントなのよ！」




／／続く（未定）